Понятно, а то меня удивил наезд на emu80 (фактически и на emu, т.к. там аналогично), а дело все же было не в эмуляторах.


Понятно, а то меня удивил наезд на emu80 (фактически и на emu, т.к. там аналогично), а дело все же было не в эмуляторах.
С любовью к вам, Yandex.Direct
Размещение рекламы на форуме способствует его дальнейшему развитию


Привнёс цвета
С уважением, Станислав.
fifan(14.09.2025), Oleg N. Cher(14.09.2025)


Показал ИИ исходники SGIDEMO. Вот такой вердикт по главной процедуре рисования линии:
Задача воспроизведения алгоритма Bresenham'а для i8080 решалась уже многократно, и я полагаю, что вылизана "от" и "до". Поделитесь пожалуйста! А за одно интересует реализация рисования окружности и эллипса по его же алгоритму.Код:; ================================================== ; === ФУНКЦИЯ РИСОВАНИЯ ЛИНИИ: line === ; ================================================== ; Входные параметры: ; DE = начальная точка (X,Y) — D=X, E=Y ; HL = конечная точка (X,Y) — H=X, L=Y ; Выходные параметры: ; DE, HL — не изменены (сохранены) ; Рисует прямую линию между точками на экране, используя алгоритм Брезенхэма (упрощённый) ; Использует putpixel для отрисовки пикселей. ; ; Примечание: код очень сложный, дублирующийся, с "жёстко закодированными" проверками. ; Не оптимизирован, но работает. line:
С уважением, Станислав.


Прошу прощения за то, что приведу ссылку на свой пост со ссылками на две процедуры рисования линий, но в том посте есть комментарии.
Если Брезенхем не обязателен, то окружности и компания (1, 2).
Еще в прекрасме можно нажать на рыбу и выбрать процедуру, но там вроде не всё самое последнее.
CityAceE(15.09.2025)


А про алгоритм Минчера там есть? Вот тема была: https://zx-pk.ru/threads/25602-algor...r-1/page2.html
Интересно, что чуть ниже (18-й пост) тоже похожий алгоритм, но без умножения на 4, чуть кривовато, но всё равно окружность.


Из нетрадиционных алгоритмов для окружностей пробовал "метод Jesko" из английской вики, он немного быстрее Мичнера, но при маленьких радиусах менее круглые окружности.


А, ну очень похоже на метод Jesko. Вот, например из вики (с учётом того, что я избавился от переменной t2):
А вот из темы по моей ссылке:Код:t1 = r / 16 x = r y = 0 Repeat Until x < y Pixel (x, y) y = y + 1 t1 = t1 + y If t1 >= x t1 = t1 - x x = x - 1
Разница лишь в том, что не учитывается 1/16 радиуса, и переменная t1 работает в сторону уменьшения (не от нуля до х, а наоборот). Ну и х уменьшается до использования корркекции t1.Код:t1 = r x = r y = 0 Repeat Pixel (x, y) y = y + 1 t1 = t1 - y If t1 < 0 x = x - 1 t1 = t1 + x Until x < y
Может это и есть причина "кривоватости" того алгоритма.
- - - Добавлено - - -
Интересно, можно ли так вычерчивать эллипс?
- - - Добавлено - - -
К примеру:
1. доработать алгоритм, чтобы он вычерчивал 1/4, а не 1/8
2. покрутить с константами при увеличении/уменьшении t1
- - - Добавлено - - -
По первому пункту:
- - - Добавлено - - -Код:t1 = r/2 x = r y = 0 Repeat Pixel (x, y) If t1 >= 0 y = y + 1 t1 = t1 - y If t1 < 0 x = x - 1 t1 = t1 + x Until x < 0
Почему-то коэффициент сжатия нужно удваивать...Код:function ellipse(r,k) { let t1=r/2,x=r,y=0; while(x>=0) { pset(x,y); if(t1>=0) { ++y; t1-=y*k; } if(t1<0) { --x; t1+=x; } } } ellipse(80,4); ellipse(40,1);
- - - Добавлено - - -
Код:function ellipse(r,ky,kx) { let t1=r/2,x=r,y=0; while(x>=0) { pset(x,y); if(t1>=0) { ++y; t1-=y*ky; } if(t1<0) { --x; t1+=x*kx; } } } ellipse(40,1,1); ellipse(80,1,1); ellipse(80,2,1); ellipse(80,4,1); ellipse(40,1,2); ellipse(40,1,4);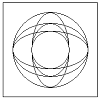
Последний раз редактировалось b2m; 15.09.2025 в 16:15.




Дык окружность тоже без умножения. Мичнер с умножением для эллипса не нашёл.
- - - Добавлено - - -
Для эллипса тоже есть?
- - - Добавлено - - -
От умножения в цикле можно избавиться:
Код:function ellipse(r,ky,kx) { let t1=r/2,x=r,y=0,ty=0,tx=kx*r; while(x>=0) { pset(x,y); if(t1>=0) { ++y; ty+=ky; t1-=ty; } if(t1<0) { --x; tx-=kx; t1+=tx; } } }
ivagor(15.09.2025)


Этот вариант мне понравился, только не понял насчет kx. Или я ошибся или kx это коэффициент увеличения по y? А ky - коэффициент сжатия по y?
Ссылки я тут приводил.
Эту тему просматривают: 1 (пользователей: 0 , гостей: 1)